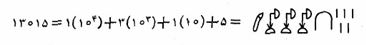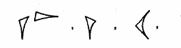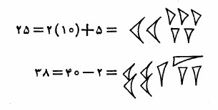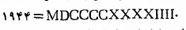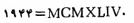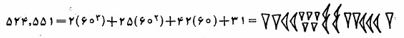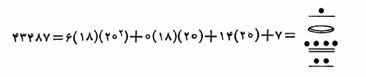تاریخ ریاضیات - فصل اول - دستگاههای عدد نویسی - بخش دوم - دستگاههای گروه بندی ساده

یکی از قدیمیترین مثالهای دستگاه گروه بندی ساده دستگاه هیروگلیفی مصری است که از حدود ۳۴۰۰. پ. م به کار می‌رفته و عمدتاً مصریان آن را در کتیبه‌هایی که روی سنگ می‌نوشته‌اند مورد استفاده قرار می‌دادند.

تاریخ ثبت: (1402/04/26 ) تاریخ بروزآوری: (1402/04/27 )

این مطلب (1,225) بار مطالعه شده است.

این مطلب را با دوستان خود در واتساپ به اشتراک بگذارید.

۴-۱ دستگاههای گروه بندی ساده

شاید تقریباً قدیمیترین دستگاه شمارش که تکوین یافته همان باشد که دستگاه گروه بندی ساده نامیده شده است. در این دستگاه عددی مانند $b$ برای پایۀ اعداد انتخاب و علایمی برای $b^3 , b^2 , b ,1$ ، و الی آخر اختیار می‌شود سپس هر عدد با استفاده از این علایم به طور جمعی بیان می‌گردد و هر علامتی به دفعات مورد لزوم تکرار می‌شود. مثال زیر اصل مندرج در آن را روشن می کند.

یکی از قدیمیترین مثالهای دستگاه گروه بندی ساده دستگاه هیروگلیفی مصری است که از حدود ۳۴۰۰. پ. م به کار می‌رفته و عمدتاً مصریان آن را در کتیبه‌هایی که روی سنگ می‌نوشته‌اند مورد استفاده قرار می‌دادند. گرچه گاهی برای نوشتن روی چیزهایی غیر از سنگ نیز از خط هیروگلیفی استفاده می‌شد مصریان به زودی دو شیوه نوشتن نسبتاً سریعتر را برای کار روی پاپیروس، چوب و سفال ابداع کردند. قدیمیترین این دو، خطی بود با حروف پیوسته موسوم به خط هیراتی (hieratic) خط کاهنان که از خط هیر و گلیفی مشتق شده و مورد استفاده روحانیت بود بعد از هیراتی خط دموتی (demotic) [خط عوام] پدید آمد، که کار برد همگانی یافت دستگاههای شمار هیراتی و دموتی از نوع گروه بندی ساده نیستند.

دستگاه شمارش هیروگلیفی مصری مبتنی بر پایۀ ۱۰ است، علایم اختیار شده برای ۱ و چند توان اول ۱۰ چنین اند.

حال هر عدد را می‌توان با استفاده از این علایم به طور جمعی بیان کرد که در آن هر علامتی به تعداد دفعات مورد لزوم تکرار می‌شود. مثلاً:

ما این عدد را از چپ به راست نوشته‌ایم اگر چه مصریان بیشتر عادت داشتند که از راست به چپ بنویسند. بابلیان قدیم که پاپیروس نداشتند و به سنگهای مناسب دسترسی کمی داشتند، برای نوشتن عمدتاً از گل رس استفاده میکردند آنان کتیبه را به وسیله فشردن قلمی که نوك آن به شکل مثلث متساوی الساقین تیزی بود بر يك لوح گل رس مرطوب نقش می کردند. با کمی کج کردن قلم از حالت قائم این امکان وجود داشت که زاوية رأس يا زاوية مجاور به قاعده مثلث متساوی الساقین بر گل رس نقش شود که بدین ترتیب دو نوع نشانه گوه - شکل (میخی) به وجود می‌آمد. سپس لوح آماده در کوره‌ای پخته می شد تا به درجه‌ای از سختی برسد که در مقابل گذشت زمان مقاوم و به يك سند دایمی بدل شود. بر روی لوحهای میخی که به فاصله زمانی ۲۰۰۰ پ.م. تا ۲۰۰ پ.م تعلق دارند اعداد کوچکتر از ۶۰ به كمك دستگاه گروه بندی ساده‌ای به پایه‌ی ۱۰ بیان شده‌اند و جالب اینکه عمل نوشتن اغلب با استفاده از علامت تفریق ساده شده است علامت تفریق و علایم به کار رفته برای ۱ و ۱۰ از چپ به راست عبارت اند از:

که در آن علامت به کار رفته برای ۱ و دو قسمتی که علامت تفریق را می‌سازند با استفاده از زاویه رأس مثلث متساوی الساقین به دست آمده‌اند و علامت به کار رفته برای ۱۰ با استفاده از یکی از زوایای مجاور به قاعده حاصل شده است به عنوان مثالهایی از اعداد نوشتاری که از این علایم در آنها استفاده شده داریم:

روشی که بابلیها برای نوشتن اعداد بزرگتر به کار می‌بردند در بخش ۱-۷ بررسی خواهد شد. شمارشهای یونانی آتیکی(Attic) یا هرودینی که پیش از قرن سوم قبل از میلاد ظهور یافتند و دستگاه گروه بندی ساده ای بر مبنای ۱۰ تشکیل می‌دهند و به روایتی تدوینگر آن هرودین(Herodian) یونانی که در حدود سال ۱۷۰ پیش از میلاد در رم دستور زبان درس می‌داده است، از آثار معروفش قاموس زبان یونانی آتن است. هرودینی از حروف اول نامهای عددی ساخته شده اند علاوه بر علایم I،∆،H،X،M برای $10^4, 10^3 , 10^2 , 10 , 1$ ، علامت خاصی برای ۵ وجود دارد این علامت خاص شکلی قدیمی از ∏ است که حرف اول کلمه یونانی پنته (pente پنج) است و ∆ حرف اول دکا (deka ده) یونانی است. سایر علایم را نیز می‌توان به همین نحو توضیح داد از علامت به کار رفته برای ۵، اغلب هم به طور منفرد و هم در ترکیب با سایر علایم استفاده می‌شد تا نمایش عددی کوتاهتر شود. به عنوان مثال در این دستگاه شمار داریم.

که در آن می‌توان علامت خاص برای ۵ را كه يك بار تنها و دوبار در ترکیب با سایر علایم ظاهر شده، تشخیص داد.

به عنوان آخرین مثال دستگاه گروه بندی ساده، باز هم در پایه‌ی ۱۰، شمارهای آشنای رومی را داریم. در اینجا به علایم اصلیI، X ،C،M برای $10^3 , 10^2 , 10 , 1$ علایم، V ، L و D برای ۵۰،۵ و ۵۰۰ افزوده می‌شوند. اصل تفریق، که مطابق آن وقتی علامتی برای واحد کوچکتر قبل از علامت به کار رفته برای واحد بزرگتر قرار گیرد، معنی تفاضل این دو واحد را دارد فقط به ندرت در دوره های باستان و میانه به کار می‌رفت. استفاده کاملتر این اصل در اعصار جدید معمول گردید به عنوان مثال در این دستگاه داریم

یا در اعصار جدیدتر، با متداول شدن اصل تفریق،

در کوششهایی که برای توضیح ریشه های دستگاه اعداد رومی می‌شود، حدس و گمان نیز بی دخالت نبوده است یکی از توضیحات موجه تر که مورد قبول عده زیادی از صاحب نظران در تاریخ لاتین و علم کتیبه خوانی است این است که I، II، III ، IIII از شکل انگشتان بلند شده گرفته شده‌اند. علامت X هم ممکن است ترکیبی از دو V باشد یا شاید از شکل دستها یا انگشتان صلیب شده به ذهن راه یافته باشد، یا شاید هم ناشی از این عادت رایج بوده باشد که موقع شمارش با پاره خطها، خطی برروی گروههای ده تایی می‌کشیده‌اند. شواهدی در دست است که علایم اصلی برای ۵۰، ۱۰۰ و ۱۰۰۰ احتمالاً آواهای دمیده‌ی یونانی Ψ(پسی) وθ (تتا)، و Φ (في) بوده‌اند. اشکال قدیمی برای پسی

بوده‌اند که همۀ آنها در کتیبه‌های اولیه به جای ۵۰ به کار رفته‌اند. علامت θ برای ۱۰۰ احتمالاً بعدها به علامت C که تا حدودی مشابه آن است تحول یافت؛ و این حقیقت که حرف اول كلمة لاتين منتوم ( centum «صد») است در این امر تأثیر داشته است. يك علامت متداول در قدیم برای ۱۰۰۰ ، 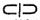است که شاید صورت دیگری از Φ باشد. تحت تأثیر این امر که M حرف اول کلمه لاتین میله (mille «هزار») است، علامت مورد استفاده برای ۱۰۰۰ به صورت M در آمد، پانصد به خاطر اینکه نصف ۱۰۰۰ است با نمایش داده شد، که بعدها به D بدل گردید کاربرد علایم و برای ۱۰۰۰ و ۵۰۰ تا سال ۱۷۱۵ مشاهده شده است.

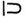
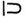
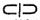
۵-۱ دستگاههای گروه بندی ضربی

مواردی وجود دارند که در آنها يك دستگاه گروه بندی ساده به آنچه شاید بتوان آن را دستگاه گروه بندی ضربی نامید، تحول یافته است. در چنین دستگاهی بعد از انتخاب پایه ، علایمی برای ۱، ۲، ...، ۱ - b و مجموعه علایمی برای 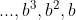$... , b^3 , b^2 , b$ اختیار می‌شوند از علایم این دو مجموعه به طور خوبی برای نشان دادن اینکه چند واحد از گروههای بالاتر مورد نیازند استفاده می‌شود. مثلاً اگر نه عدد اول را با علایم معمولی نشان دهیم ولی ۱۰۰،۱۰ ،۱۰۰۰ را مثلا با a و b و c نشان دهیم در این صورت در دستگاه شمار ضربی می نویسیم

5625=5c6b2a5

دستگاه شمار سنتی چینی - ژاپنی يك دستگاه گروه بندی ضربی در پایه ۱۰ است. علایم دو گروه اساسی و عدد ۵۶۲۵ که عمودی نوشته می‌شوند، به صورت زیرند:

۶-۱ دستگاههای شمارش رمزی

در يك دستگاه شمارش رمزی، بعد از اينكه يك پایه‌ی b انتخاب گردید علایمی برای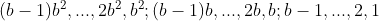 $(b-1)b^2 , ... , 2b^2 , b^2 ; (b-1)b , ... , 2b , b ; b-1,...,2,1$ ؛ و غيره اختیار می‌شود. اگرچه در چنین دستگاهی علایم زیادی باید به حافظه سپرده شود، نمایش اعداد در آن فشرده است.

دستگاه شمارش یونانی به اصطلاح یونیایی(Ionic) ،یا الفبایی، از نوع رمزی است و می توان رد آن را تا ۴۵۰ پ.م پیگیری کرد این دستگاه در پایه ١0 است و در آن از ۲۷ نشانه ۲۴ حرف الفبای یونانی همراه با علایم حروف منسوخ دیگاما (digamma)، کوپا (koppa) و سامپی (sampi) استفاده می‌شود. گرچه در این دستگاه از حروف بزرگ استفاده می‎شد و حروف كوچك خيلى دیرتر جانشین آنها گردیدند در اینجا دستگاه را با حروف كوچك شرح خواهیم داد. معادله‌ای زیر باید به حافظه سپرده می شدند:

به عنوان مثالهایی از موارد کاربرد این علایم داریم:

$\iota \beta =12 , \kappa \alpha =21 , \sigma \mu \zeta = 247$

برای مشخص کردن اعداد بزرگ، از تیره‌ها و آکسانهایی که همراه حروف به کار می‌رفت استفاده می‌شد.

علامتهای حروف منسوخ دیگاما، کوپا و سامپی به ترتیب زیرند.

سایر دستگاهها با شمارش رمزی عبارت‌اند از هیراتی و دموتی مصری، قبطی، هندی برهمایی، عبری، سوری و عربی بدوی سه تای آخر مانند یونانی یونیایی، دستگاههای شمارش رمزی الفبایی هستند.

۷-۱ دستگاههای شمارش موضعی

دستگاه شمارش کنونی، نمونه‌ای از يك دستگاه شمارش موضعی با پایۀ ۱۰ است. برای چنین دستگاهی بعد از انتخاب پایۀ علایم اصلی برای $b-1,...,2,1,0$ اختیار می‌شوند. بنابر این b علامت اصلی وجود دارند که غالباً در دستگاه معمولی امروزی ارقام نامیده می‌شوند. حال هر عدد (طبیعی) N را میتوان به طور یکتا به صورت:

$N=a_{n}b^{n}+a_{n-1}b^{n-1}+...+a_{2}b^{2}+a_{1}b+a_{0}$

نوشت که در آن $i=0,1,2,...,n ; 0\leqslant a_{1}< b$ . سپس عدد N را در پایه b با رشته‌ای از علامتهای اصلی به صورت

$a_{n}a_{n-1}...a_{2}a_{1}a_{0}$

نشان می‌دهیم. از این رو هر علامت اصلی در هر عدد مفروض، نمایش مضرب توانی از پایه است و این توان به موضعی بستگی دارد که علامت اصلی در آن ظاهر می‌شود. مثلا در دستگاه شمارش هندی - عربی ۲ در ۲۰۶ نشانه‌ی $2(10^2)$ ، یا ۲۰۰ است، در حالی که در ۲،۲۷ نشانه (۱۰) ۲ یا ۲۰ است باید توجه داشت که برای وضوح کامل، علامتی برای صفر مورد نیاز است تا توانهایی از پایه را که ممکن است وجود نداشته باشند، نشان دهد. هر دستگاه شمارش ،موضعی محصول منطقى ولى نه لزوماً تاريخى يك دستگاه گروه بندی ضربی است.

بابلیهای قدیم در بین سالهای ۳۰۰۰ و ۲۰۰۰ پ. م. يك دستگاه شصتگانی پدید آوردند که از اصل ارزش موضعی استفاده می‌کرد مع‌هذا این دستگاه شمارش در واقع مختلط است زیرا گرچه اعداد بزرگتر از ۶۰ بر طبق اصل ارزش موضعی نوشته می‌شوند اعداد درون گروه ۶۰ تایی اصلی، مطابق آنچه در بخش ۱-4 تشریح شد، به كمك يك دستگاه گروه بندی ساده در مبنای ۱۰ نوشته می‌شوند به عنوان مثال داریم:

این دستگاه شمارش موضعی، تا بعد از سال ۳۰۰ پ.م علامتی برای صفر نداشت. ابهامی را که از این امر در لوحهای گلی پدید می‌آید غالباً می‌توان تنها با مطالعه دقیق متن بر طرف کرد. آنچه بسیار جالب توجه است دستگاه شمارش مایایی، با مبدئی دور و نامعلوم، است که توسط هیئتهای اعزامی اسپانیایی به یوکاتان (Yucatán) در اوایل قرن شانزدهم کشف شد. این دستگاه اساساً بیست بیستی است بجز اینکه گروه عددی دوم به جای اینکه $20^2 = 400$ باشد، ۳۶۰ (۲۰)۱۸ است گروههای بالاتر به صورت $18(20^{^{2}})$ هستند. توضیح این اختلاف احتمالاً در این حقیقت نهفته است که سال رسمی مایایی از ۳۶۰ روز تشکیل می‌شد. علامت صفر که در جدول زیر داده شده یا صورت دیگری از این علامت پیوسته مورد استفاده قرار می‌گیرد اعداد درون گروه ۲۰ تایی اصلی به صورتی بسیار ساده با استفاده از نقطه و خط تیره (سنگریزه و تکه چوب) بر طبق طرح گروه بندی ساده زیر نوشته می‌شوند که در آن نقطه نمایش ۱ و خط تیره نمایش ۵ است.

مثالی از يك عدد بزرگ که به روش عمودی مایایی نوشته شده، در زیر نشان داده می‌شود:

دستگاه مختلط پایه‌ای که شرحش را دادیم، مورد استفاده طبقه روحانیون بود. گزارشهایی از يك دستگاه بیست بیستی خالص در دست است که مورد استفاده مردم عادی بود ولی به صورت نوشته باقی نمانده است.

برچسب: تاریخ ریاضیات; تاریخ علم; شمارش
اثر یا گردآوری: 1- هاورد . و ایوز - مترجم : دکتر محمد قاسم وحیدی اصل، 2- جورج سارتون;منبع: 1- آشنایی با تاریخ ریاضیات و 2- تاریخ علم - لینک منابع: -

لطفا در صورت تمایل نظر خود را در رابطه با این مطلب از راه واتساپ به ما ارائه نمائید.

تاریخ ریاضیات

تاریخ علم

شمارش

آخرین مطالب مرتبط:

تاریخ ریاضیات - فصل اول - دستگاههای عدد نویسی - بخش نخست

نگاهی به تاریخ علم؛ فصل دوم: از سنگ تا فلز (د – نوسنگی)

نگاهی به تاریخ علم؛ فصل دوم: از سنگ تا فلز (ج – دوران میان سنگی، بخش دوم؛ هنر و نقاشی)

نگاهی به تاریخ علم؛ فصل دوم: از سنگ تا فلز (ج – دوران میان سنگی، بخش اول)

نگاهی به تاریخ علم؛ فصل دوم: از سنگ تا فلز (ج – دوران پارینه‌سنگی پایانی)

نگاهی به تاریخ علم؛ فصل دوم: از سنگ تا فلز (ب – دوران پارینه‌سنگی میانی)

نگاهی به تاریخ علم؛ فصل دوم: از سنگ تا فلز (الف – دوران پارینه‌سنگی پیشین)

نگاهی به تاریخ علم؛ فصل اول: پیدایش خط (ب – اختراع الفبا)

نصر و تاریخ علم تمدن اسلامی

1403/09/01 10:08

در زمینه‌ی انتشار نظرات مخاطبان رعایت چند مورد ضروری است:

لطفاً نظرات خود را با حروف فارسی تایپ کنید.
«انجمن خرد» مجاز به ویرایش ادبی نظرات مخاطبان است.
انجمن خرد از انتشار نظراتی که حاوی مطالب کذب، توهین یا بی‌احترامی به اشخاص، قومیت‌ها، عقاید دیگران، موارد مغایر با قوانین کشور و آموزه‌های دین مبین اسلام باشد معذور است.
درج در قسمت هایی که با ستاره قرمز مشخص گردیده الزامی است.
تعداد کاراکترهای نام، ایمیل و نظر نباید به ترتیب بیش از 100، 300 و 500 بیشتر باشد . در صورت عدم رعایت متاسفانه نظر شما ثبت نخواهد گردید.
نظرات پس از تأیید مدیر سایت منتشر می‌شود.

نام:

پست الکترونیک:

متن نظر:

کد امنیتی: